Для приготування чайної суміші змішують індійський та цейлонський чай у співвідношенні 9:11. Який відсоток у цій суміші становить цейлонський чай?
Після проведення контрольної роботи з математики в одному з класів було отримано такі результати. Знайдіть середній бал за контрольну роботу.
| Оцінки (бал) | 2 | 3 | 4 | 5 |
| Кількість учнів | 3 | 8 | 10 | 4 |
Підставою циліндра є
Обчисливши ![]()
На малюнку зображено трикутник ABC, у якому ∠ ACB = 37°, ∠ AMN = 107°. Використовуючи дані малюнка, знайдіть градусну міру кута BAC.
Розв’яжіть рівняння 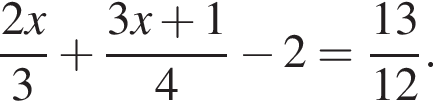
На рисунку зображено графік функції
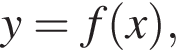 яка визначена на відрізку [−4; 3]. Укажіть область значень цієї функції.
яка визначена на відрізку [−4; 3]. Укажіть область значень цієї функції.
Розкладіть на множники вираз 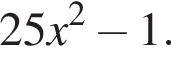
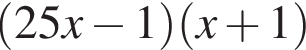

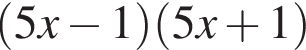
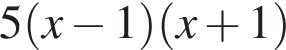
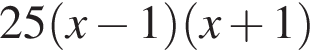
Які з наведених тверджень є правильними?
I. градусна міра розгорнутого кута дорівнює 180°.
II. У рівнобедреному трикутнику бісектриса, проведена до основи, є медіаною і висотою.
III. Площу рівностороннього трикутника можна знайти за формулою 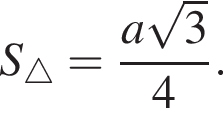
Результат спрощення виразу 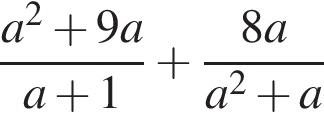 має вид:
має вид:
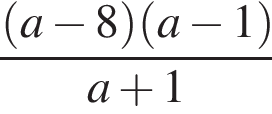
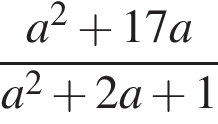
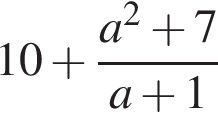
Вкажіть номер малюнка, на якому показано розв’язок системи нерівностей 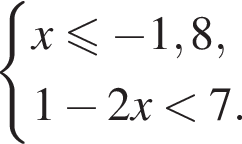
Сторони підстави правильної чотирикутної піраміди дорівнюють 10, бічні ребра дорівнюють 13. Знайдіть площу поверхні цієї піраміди.
Розв’яжіть рівняння 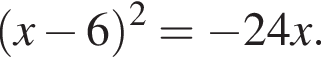
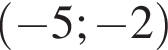
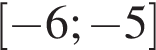
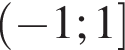
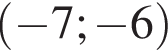
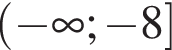
В прямоугольном треугольнике ABC катет
 а высота CH, опущенная на гипотенузу, равна
а высота CH, опущенная на гипотенузу, равна ![]() Найдите
Найдите 
Використовуючи формулу Ньютона-Лейбніца, обчисліть 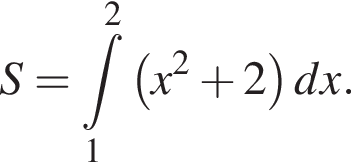
На рисунках (1−3) зображено графіки функцій, визначених на відрізку [−4; 4].
До кожного п очатку речення (1−3) доберіть його закінчення (А−Д) так, щоб утворилося правильне твердження.
1. Функція, графік якої зображ ено на рис. 1,
2. Функція, графік якої зображ ено на рис. 2,
3. Функція, графік якої зображ ено на рис. 3,
А рис. є непарною.
Б рис. набуває найбільшого значення, що дорівнює 4.
В рис. є парною.
Г рис. має три нулі.
Д рис. має дві точки локального екстремуму.
До кожного початку речення (1−3) доберіть його закінчення (А−Д) так, щоб утворилося правильне твердження.
1. Сума чисел 32 і 18
2. Добуток чисел 32 і 18
3. Частка чисел 32 і 18
А є квадратом натурального числа
Б є числом, що ділиться наділо на 10
В є найменшим спільним кратним чисел 32 і 18
Г є раціональним числом, яке не є цілим
Д є дільником числа 84
У довільній трапеції ABCD середня лінія MN дорівнює 10 см, а відрізок LK, що з'єднує середини діагоналей, дорівнює 3 см. Висота трапеції ABCD дорівнює 6 см.
Встановіть відповідність між відрізками (1-3) і їх довжинами (А−Д).
1 AD
2 BC
3 висота трапеції AMND
А 5 см
Б 7 см
В 3 см
Г 13 см
Д 6 см
Старший брат договорился с Мишей, что в пятницу он будет готовиться к экзамену по физике, решая задачи из сборника. За первую задачу брат разрешит ему поиграть на своей приставке 10 минут, а за каждую следующую задачу ему можно будет играть на 3 минуты больше, чем за предыдущую. Сколько минут можно будет поиграть Мише в воскресенье, если он решит 8 задач?
Відповідь: ,.
Довідкову інформацію промовляють почергово по одному разу п’ятьма мовами: українською, англійською, німецькою, російською та польською. Скільки всього є варіантів послідовностей озвучування цієї інформації цими п’ятьма мовами, якщо спочатку її промовляють українською?
Відповідь: ,.
В прямоугольной системе координат в пространстве заданы векторы 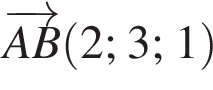 и
и  Найдите сумму координат вектора
Найдите сумму координат вектора 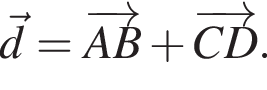
Відповідь: ,.
Определите, при каких значениях параметра a, ![]() такие, что уравнение
такие, что уравнение 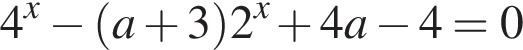 имеет ровно один корень.
имеет ровно один корень.
Відповідь: ,.

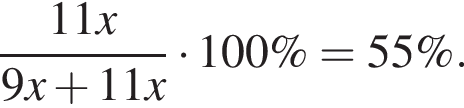
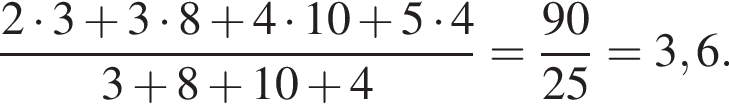
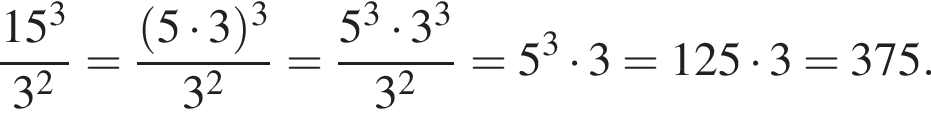
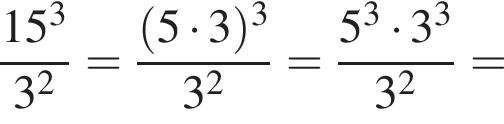
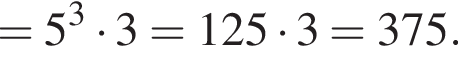
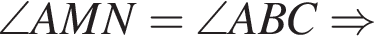
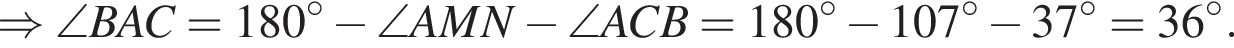
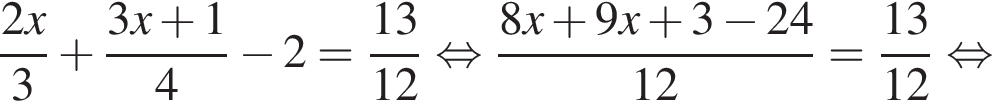

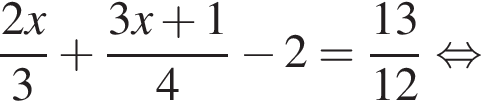
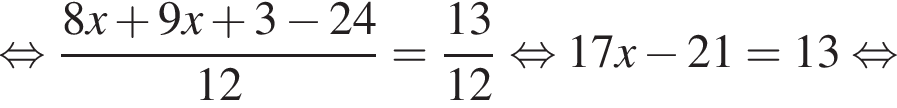

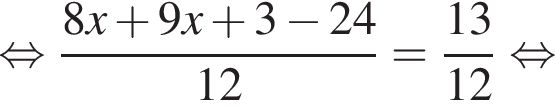
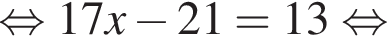
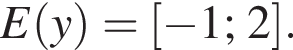
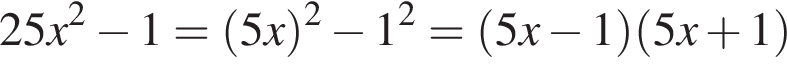
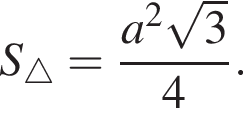
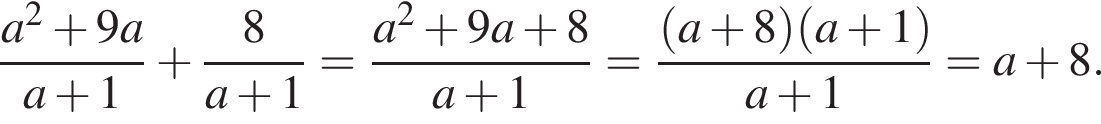
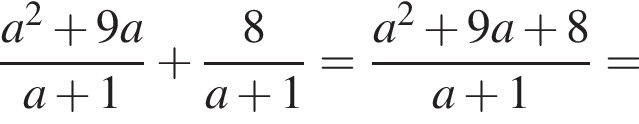
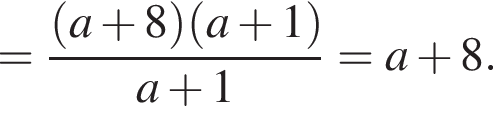
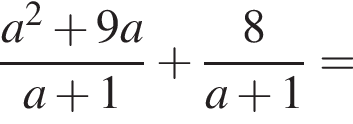
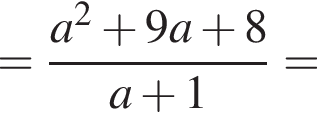
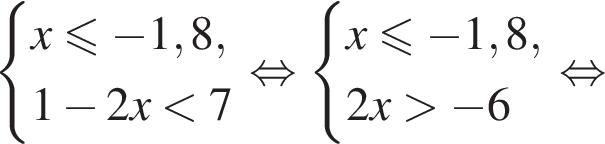
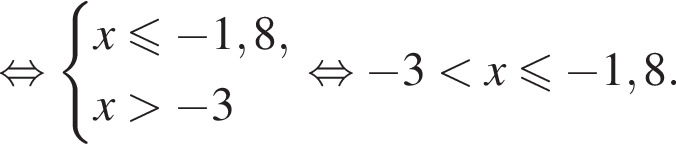
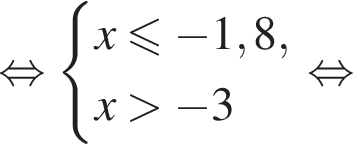
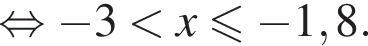
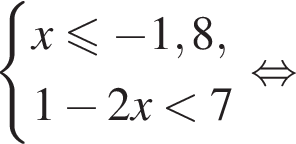
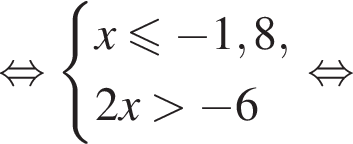

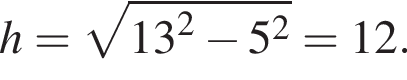 Тогда площадь поверхности пирамиды
Тогда площадь поверхности пирамиды 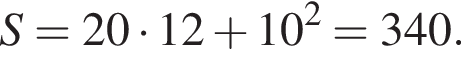
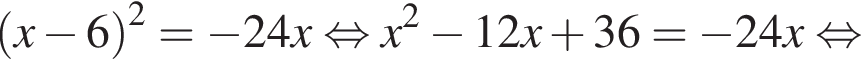
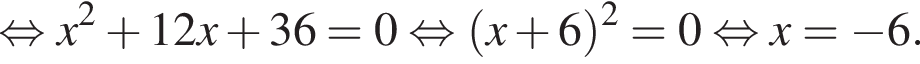
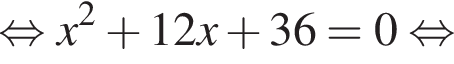
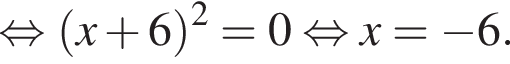
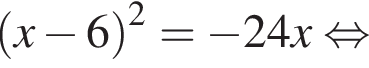
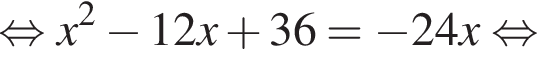
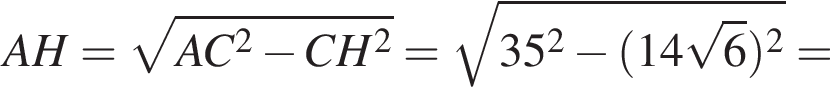
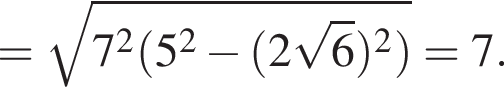
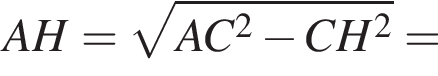
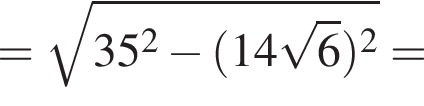
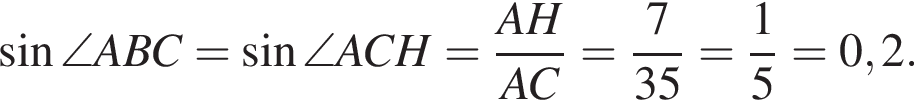

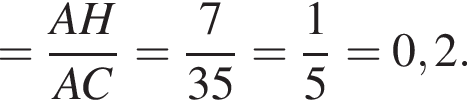
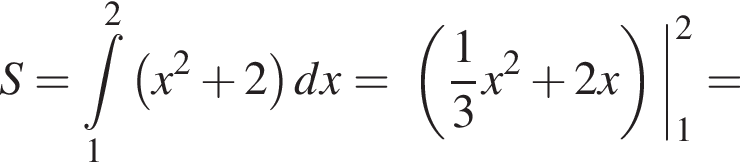
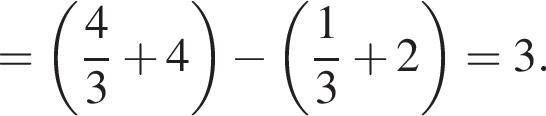
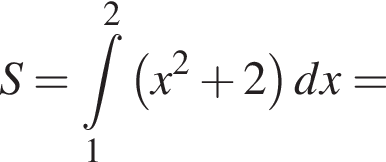
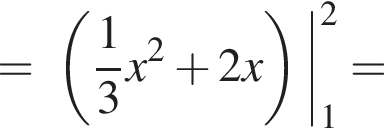
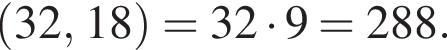 Сумма
Сумма 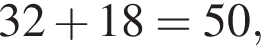 делится на 10, другими свойствами не обладает. Произведение
делится на 10, другими свойствами не обладает. Произведение  — квадрат натурального числа, другими свойствами не обладает. Частное
— квадрат натурального числа, другими свойствами не обладает. Частное 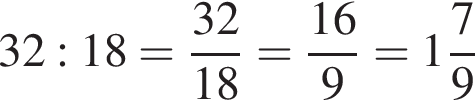
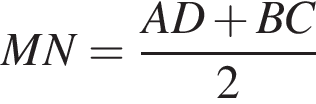 и
и 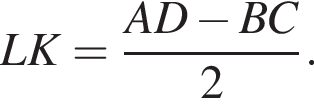 Составим и решим систему уравнений:
Составим и решим систему уравнений: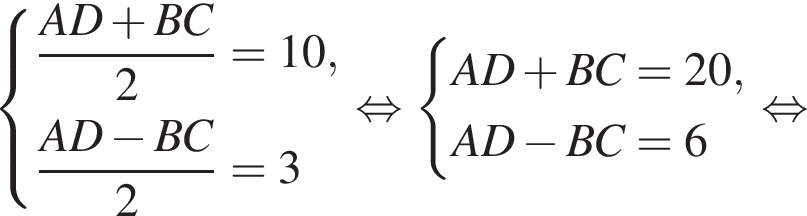
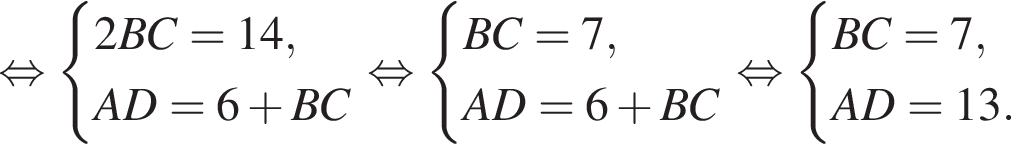
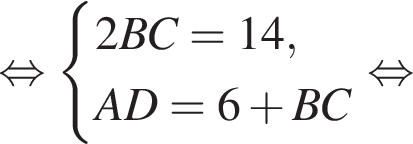
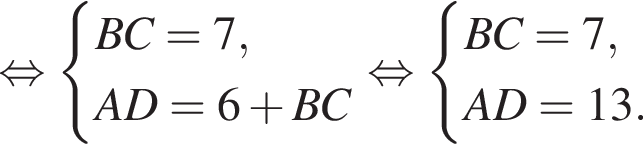
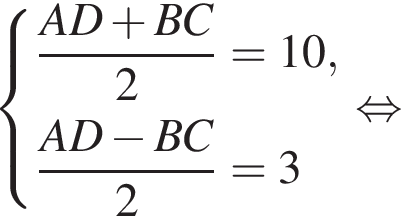
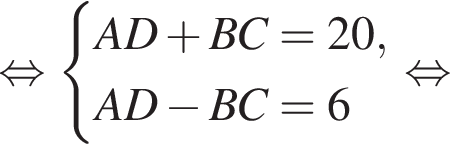
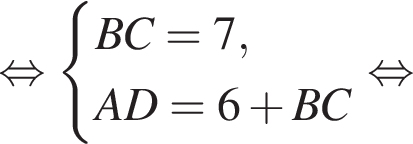
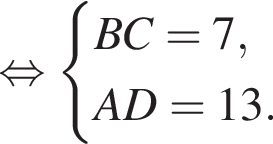
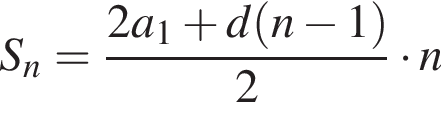 сумму арифметической прогрессии первых восьми членов:
сумму арифметической прогрессии первых восьми членов: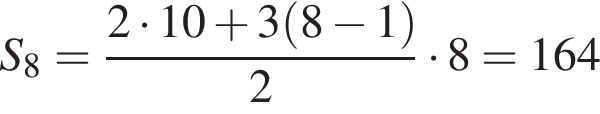 минуты.
минуты. способами.
способами.
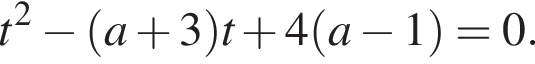 Чтобы исходное уравнение имело ровно один корень, полученное уравнение должно иметь:
Чтобы исходное уравнение имело ровно один корень, полученное уравнение должно иметь: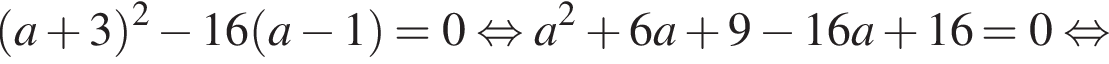

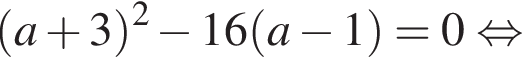

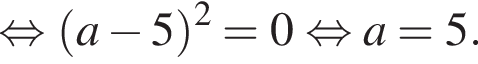
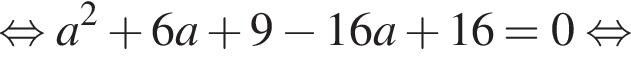
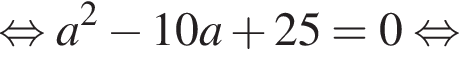
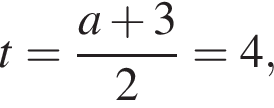 что соответствует условию положительности корня.
что соответствует условию положительности корня.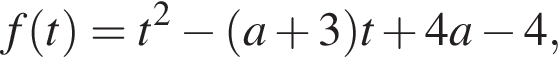 тогда
тогда 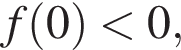 т. е.
т. е. 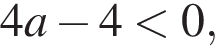 откуда
откуда 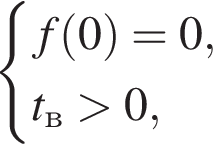 откуда
откуда 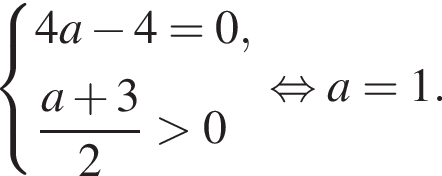
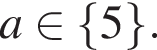
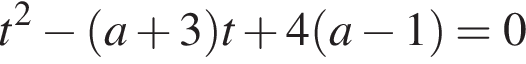 равна
равна 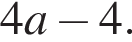 Следовательно, это числа 4 и
Следовательно, это числа 4 и