Через точку А (6; 8) проведено пряму, паралельну осі абсцис. Знайдіть ординату її точки перетину з віссю Oy.
Знайдіть ординату точки, симетричної точки A (6; 8) щодо осі Ox.
Знайдіть абсцису точки, симетричній точці A (6; 8) щодо початку координат.
Знайдіть ординату точки, симетричної точки A (6; 8) щодо початку координат.
Точка A знаходиться у вузлі сітки (див. рис).
Якщо точка B симетрична точці А щодо початку координат, то довжина відрізка АВ дорівнює:
На координатній прямій позначені точки (-2), А (6), X ( а ). Знайдіть довжину відрізка ВХ якщо точки В і X симетричні щодо точки А.
Графік функції, заданої формулою y = kx + b симетричний щодо початку координат і проходить через точку A (2; 10). Значення виразу k + b одно:
Парна функція 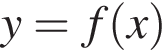 визначена на проміжку
визначена на проміжку 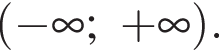 Які з наведених тверджень є правильними?
Які з наведених тверджень є правильними?
I. 
II. 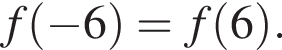
III. Графік функції 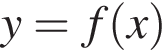 симетричний відносно осі y.
симетричний відносно осі y.
Укажіть з-поміж наведених функцію f(х), якщо для кожного х з області її визначення виконується рівність 
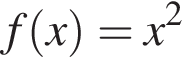
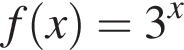
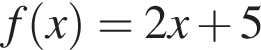

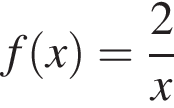
Укажіть функцію, графік якої проходить через початок координат.
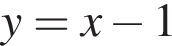
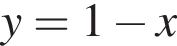
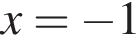
На координатній площині дано точку А і пряму l (див. рис.). Визначте координати точки, симетричної точці А відносно прямої l .
Графік функції, заданої формулою y = kx + b симетричний щодо початку координат і проходить через точку A (2; 10). Значення виразу k + b одно:
Точка A знаходиться у вузлі сітки (див. рис).
Якщо точка B симетрична точці А щодо початку координат, то довжина відрізка АВ дорівнює:
На координатній прямій позначені точки (-2), А (6), X ( а ). Знайдіть довжину відрізка ВХ якщо точки В і X симетричні щодо точки А.
Через точку А (6; 8) проведено пряму, паралельну осі абсцис. Знайдіть ординату її точки перетину з віссю Oy.
Знайдіть абсцису точки, симетричній точці A (6; 8) щодо осі Oy.
Знайдіть ординату точки, симетричної точки A (6; 8) щодо осі Ox.
Знайдіть абсцису точки, симетричній точці A (6; 8) щодо початку координат.
Знайдіть ординату точки, симетричної точки A (6; 8) щодо початку координат.

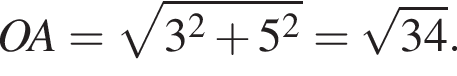
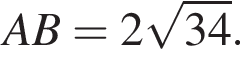
 В таком случае длина BX равна
В таком случае длина BX равна 
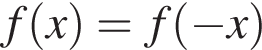 при всех x, поэтому верными являются второе и третье утверждения.
при всех x, поэтому верными являются второе и третье утверждения.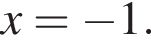 Из этих функций такой будет только последняя. И действительно, при всех x
Из этих функций такой будет только последняя. И действительно, при всех x