Учень з понеділка до п’ятниці записував час (у хвилинах), який він витрачав на дорогу до школи та зі школи (див. таблицю).
| Днi | понеділок | вівторок | середа | четвер | п’ятниця |
|---|---|---|---|---|---|
| Дорога до школи | 19 | 20 | 21 | 17 | 23 |
| Дорога зі школи | 28 | 22 | 20 | 25 | 30 |
На скільки хвилин у середньому дорога зі школи триваліша за дорогу до школи?

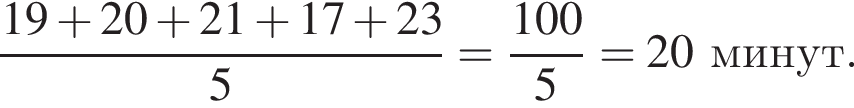
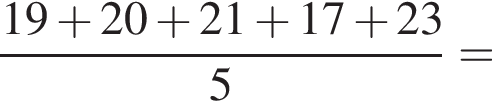
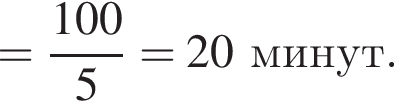
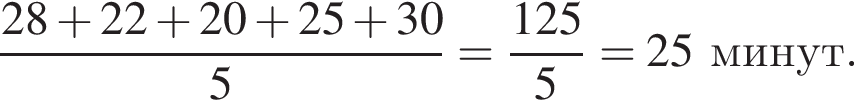
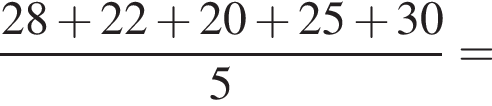
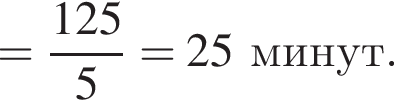
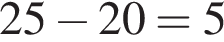 минут.
минут.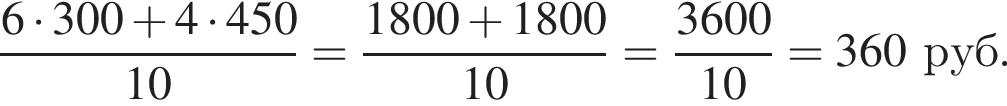
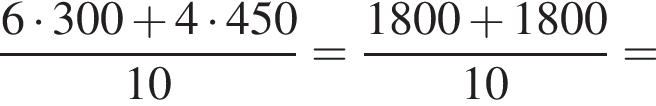
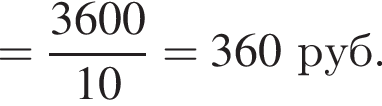
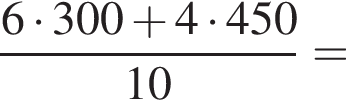
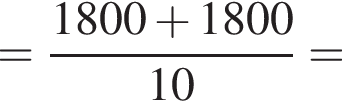
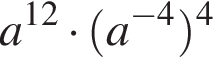 при
при 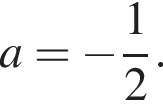
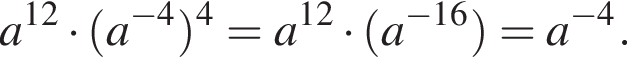
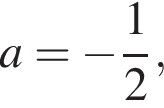 значение полученного выражения равно 16.
значение полученного выражения равно 16.
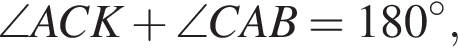 так как это односторонние углы при пересечении параллельных прямых секущей AC. Значит
так как это односторонние углы при пересечении параллельных прямых секущей AC. Значит 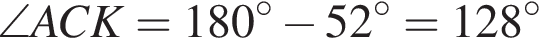 и
и 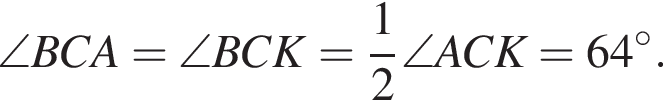
 как накрест лежащие углы при пересечении параллельных прямых секущей BC, поэтому
как накрест лежащие углы при пересечении параллельных прямых секущей BC, поэтому 
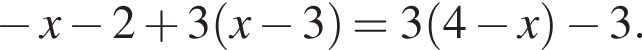

 визначеної на відрізку [−7; 7]. Користуючись рисунком, знайдіть f(2).
визначеної на відрізку [−7; 7]. Користуючись рисунком, знайдіть f(2). 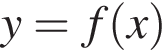 в точке
в точке 
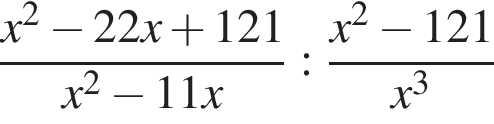 .
.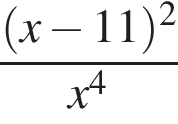
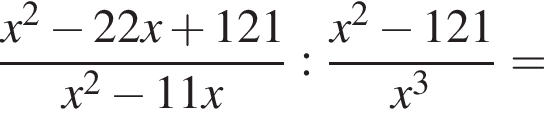
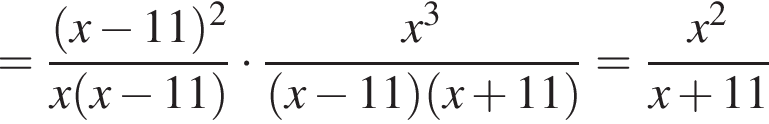
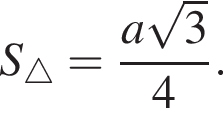
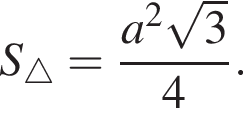
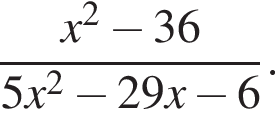
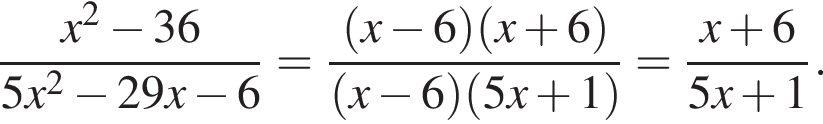
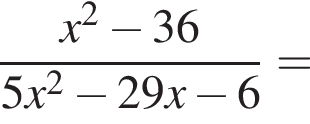
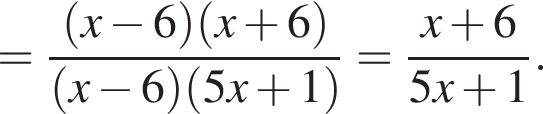
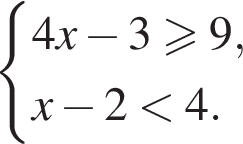


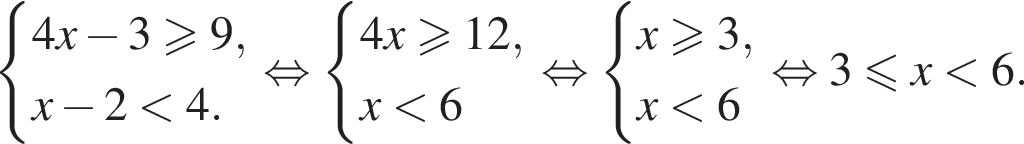
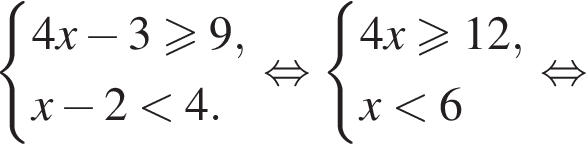
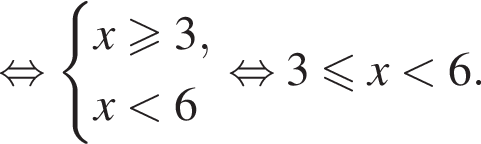
 центр основания за O, середину AB за M. Тогда
центр основания за O, середину AB за M. Тогда 
 Значит
Значит  Итак, половина расстояния между сторонами AB и CD это 24, значит само расстояние (равное стороне BC квадрата ABCD) равно 48.
Итак, половина расстояния между сторонами AB и CD это 24, значит само расстояние (равное стороне BC квадрата ABCD) равно 48.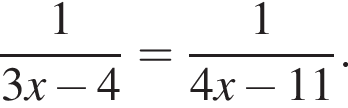
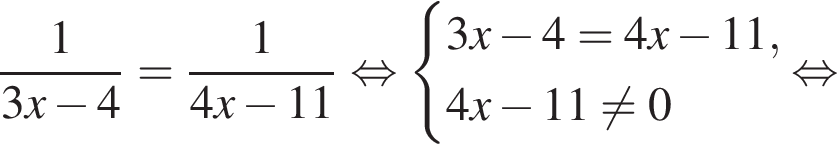
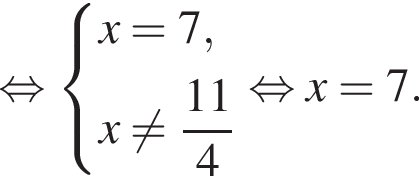
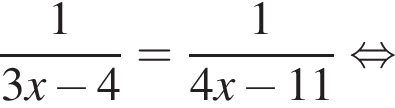
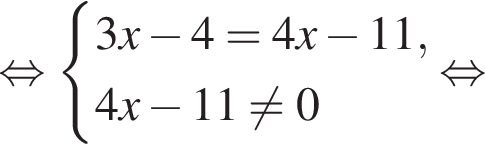
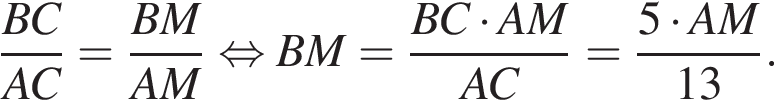
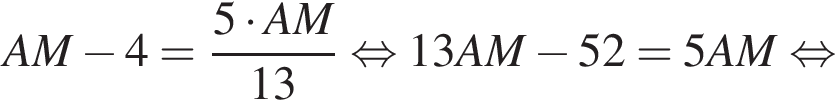
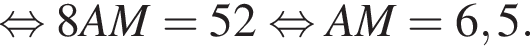
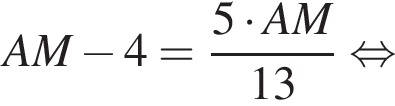

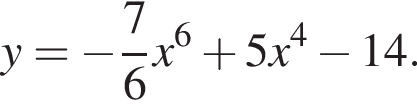
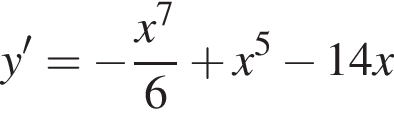
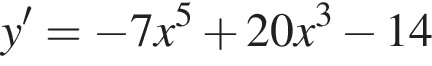
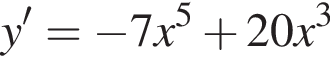
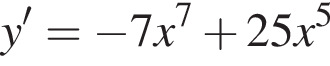
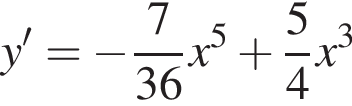
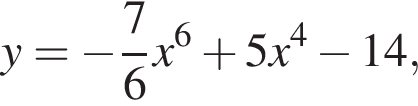 используя правило нахождения производной суммы функций:
используя правило нахождения производной суммы функций: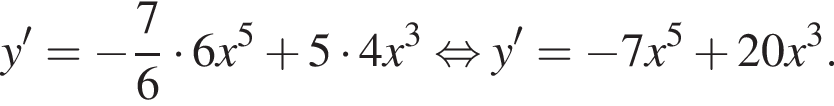
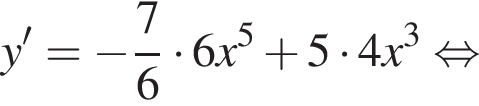
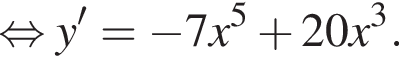
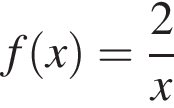
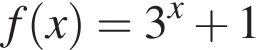
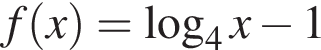
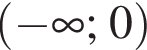

 имеет две асимптоты — прямые x = 0 и y = 0. Ответ — В.
имеет две асимптоты — прямые x = 0 и y = 0. Ответ — В.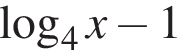 определена на промежутке
определена на промежутке  Ответ — Г.
Ответ — Г.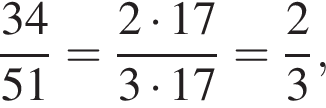 у остальных дробей числитель и знаменатель не имеют общих делителей, больших 1.
у остальных дробей числитель и знаменатель не имеют общих делителей, больших 1.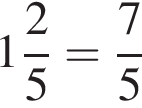 будет дробь
будет дробь 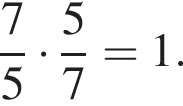
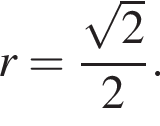 Получаем: 2 — Г.
Получаем: 2 — Г. 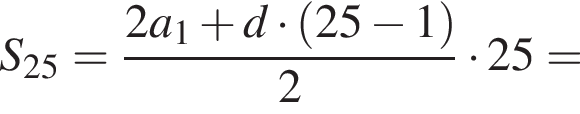
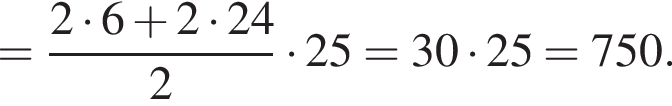
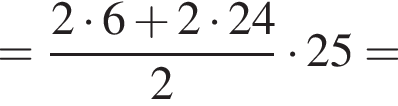


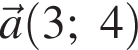 и
и 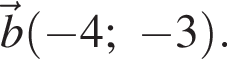 Найдите косинус угла между ними.
Найдите косинус угла между ними.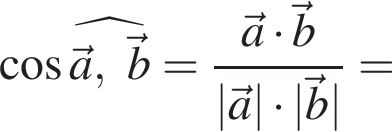
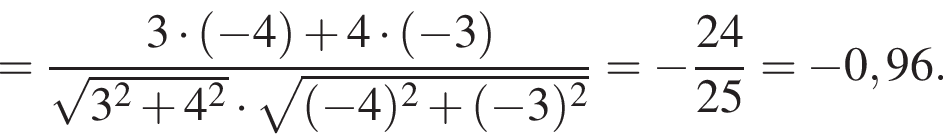
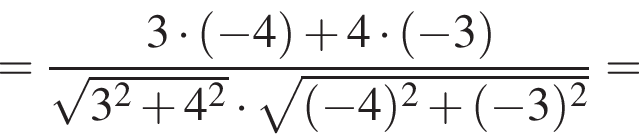
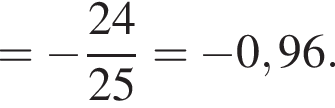
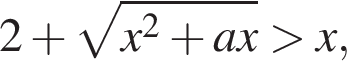 де x – змінна, a – параметр. Найдите наименьшее целое значение параметра a, при котором множество решений неравенства содержит отрезок [4; 7].
де x – змінна, a – параметр. Найдите наименьшее целое значение параметра a, при котором множество решений неравенства содержит отрезок [4; 7].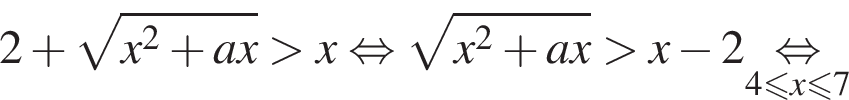
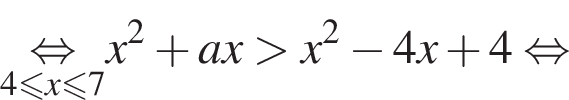
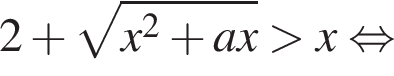
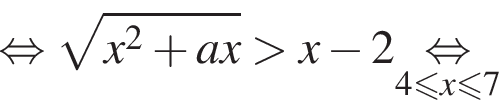
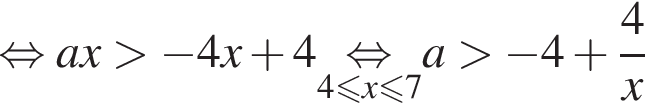
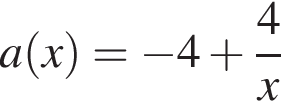 убывает. Значит, чтобы отрезок
убывает. Значит, чтобы отрезок 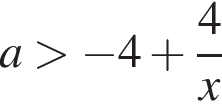 необходимо и достаточно, чтобы выполнялось неравенство
необходимо и достаточно, чтобы выполнялось неравенство 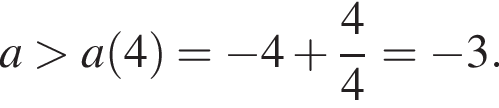 Наименьшее целое значение a равно −2.
Наименьшее целое значение a равно −2.