В арифметической прогрессии вычислите 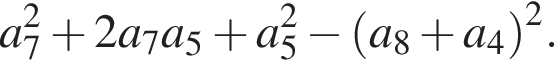
Відповідь: ,.
В арифметической прогрессии вычислите 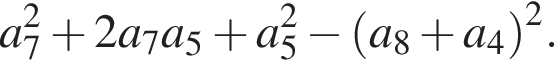
Відповідь: ,.
В арифметичній прогресії обчисліть 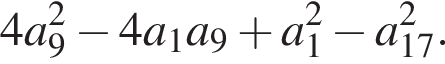
Відповідь: ,.
В арифметичній прогресії (an) третій член дорівнює 20, різниця прогресії d = –3,2. Обчисліть суму перших шести членів цієї прогресії.
Відповідь: ,.
В арифметичній прогресії (an) другий член дорівнює 18, а різниця прогресії d = 2,4. Знайдіть суму перших 7 членів прогресії.
Відповідь: ,.
У геометричній прогресії![]() відомо що
відомо що 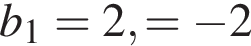 . Знайти п’ятий член цієї прогресії.
. Знайти п’ятий член цієї прогресії.
Відповідь: ,.
Геометрична прогресія ![]() задана формулою n-го члена
задана формулою n-го члена  Вкажіть четвертий член цієї прогресії.
Вкажіть четвертий член цієї прогресії.
Відповідь: ,.
Дана геометрична прогресія ( bn ), знаменник якої дорівнює 2 а 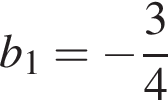 . Знайдіть суму перших шести її членів.
. Знайдіть суму перших шести її членів.
Відповідь: ,.
У геометричній прогресії сума першого та другого членів дорівнює 75, а сума другого та третього членів дорівнює 150. Знайдіть перші три члени цієї прогресії.
У відповіді запишіть перший, другий та третій члени прогресії без прогалин.
Геометрична прогресія задана умовою 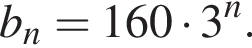 Знайдіть суму перших її 4 членів.
Знайдіть суму перших її 4 членів.
Відповідь: ,.
Виписані перші кілька членів геометричної прогресії: 17, 68, 272, … Знайдіть її четвертий член.
Відповідь: ,.
Виписано кілька послідовних членів геометричної прогресії: …; 150; x ; 6; 1,2; … Знайдіть член прогресії, позначений літерою x.
Відповідь: ,.
Виписано перші кілька членів геометричної прогресії: −1024; −256; −64; … Знайдіть суму перших 5 її членів.
Відповідь: ,.
Геометрична прогресія задана умовою  Знайдіть суму перших її 4 членів.
Знайдіть суму перших її 4 членів.
Відповідь: ,.
Виписано кілька послідовних членів геометричної прогресії: …; 1,75; x ; 28; −112; … Знайдіть член прогресії, позначений літерою x.
Відповідь: ,.
Дано геометричну прогресію ( bn ), для якої b5 = −14, b8 = 112. Знайдіть знаменник прогресії.
Відповідь: ,.
Геометрична прогресія задана умовою b1 = −7, bn + 1 = 3 bn. Знайдіть суму перших 5 її членів.
Відповідь: ,.
Дана геометрична прогресія ( bn ), знаменник якої дорівнює 5 а 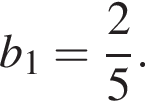 Знайдіть суму перших 6 її членів.
Знайдіть суму перших 6 її членів.
Відповідь: ,.
Дана геометрична прогресія ( bn ), для якої b3 =![]() , b6 =-196. Знайдіть знаменник прогресії.
, b6 =-196. Знайдіть знаменник прогресії.
Відповідь: ,.
Геометрична прогресія задана умовою b1 = -3, bn + 1 = 6 bn. Знайдіть суму перших 4 її членів.
Відповідь: ,.
Виписано кілька послідовних членів геометричної прогресії: …; -12; x ; -3; 1,5; … Знайдіть член прогресії, позначений літерою x.
Відповідь: ,.
Дана геометрична прогресія (bn), знаменник якої дорівнює 3, а 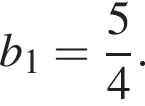 Знайдіть суму перших 6 членів прогресії.
Знайдіть суму перших 6 членів прогресії.
Відповідь: ,.
Дана геометрична прогресія (bn), знаменник якої дорівнює 2, а 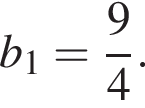 Знайдіть суму перших 11 членів прогресії.
Знайдіть суму перших 11 членів прогресії.
Відповідь: ,.