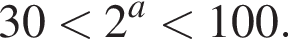Число хвойних дерев у парку відноситься до листяних як 1:4. Скільки відсотків дерев у парку складають листяні?
Зростання футболістів, які грали на полі, було 1,74 м, 1,83 м, 1,9 м, 1,81 м, 1,75 м та 2,01 м. Обчисліть середнє зростання футболістів. Відповідь округліть до сотих.
Яка постать є перерізом сфери площиною?
Обчисліть 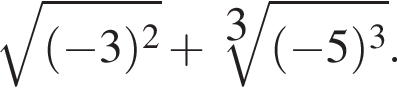
На малюнку зображені розгорнутий кут AOM та промені OB та OC. Відомо, що ∠ AOC = 102°, ∠ BOM = 128°. Знайдіть величину кута BOC.
Розв’яжіть рівняння 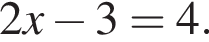
На рисунку зображено графік функції
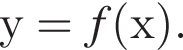 визначеної на проміжку [—3; 3]. На якому з наведених проміжків ця функція зростає?
визначеної на проміжку [—3; 3]. На якому з наведених проміжків ця функція зростає?
Спростіть вираз 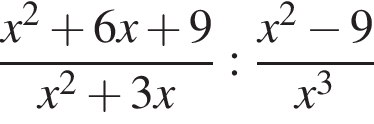 .
.
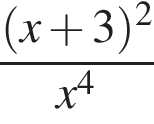
Які з наведених тверджень є правильними?
I. Якщо два кути одного трикутника дорівнюють двом кутам іншого трикутника, то такі трикутники подібні.
II. Якщо два кути трикутника рівні, то рівні також протилежні їм сторони.
III. Якщо діагоналі ромба дорівнюють 3 і 4, то його площа дорівнює 6.
Скоротіть дріб 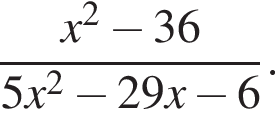
Розв'яжіть систему нерівностей 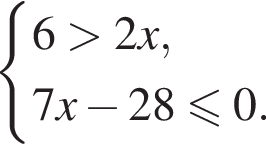
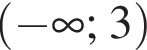
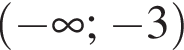
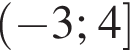
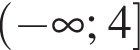
У правильній трикутній піраміді SABC точка M – середина ребра AB, S – вершина. Відомо, що BC = 3, а площа бічної поверхні піраміди дорівнює 45. Знайдіть довжину відрізка SM.
Знайдіть корінь рівняння 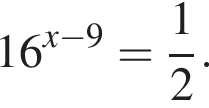
Дан треугольник ABC, в котором AC = 32. Используя данные рисунка, найдите длину стороны AB треугольника ABC.
Укажіть похідну функції 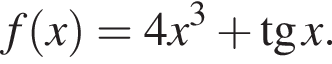
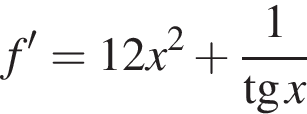
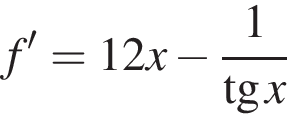
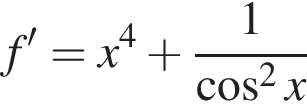
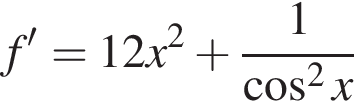
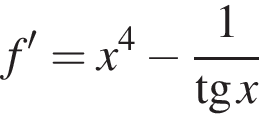
До кожного початку речення (1−3) доберіть його закінчення (А−Д) так, щоб утворилося правильне твердження.
1. Функція 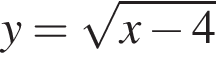
2. Функція 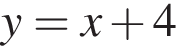
3. Функція ![]()
А спадає на проміжку 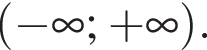
Б не визначена в точці x = 1.
В є парною.
Г набуває додатного значення в точцi x = −3.
Д є непарною.
Установіть відповідність між виразом (1–3) та проміжком (А–Д), якому належить його значення.
1 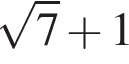
2 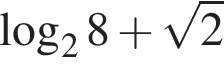
3 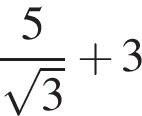
А ![]()
Б ![]()
В ![]()
Г ![]()
Д ![]()
Основи ВС й AD рівнобічної трапеції ABCD дорівнюють 7 см і 25 см відповідно. Діагональ трапеції BD перпендикулярна до бічної сторони АВ. До кожного початку речення (1—3) доберіть його закінчення (А—Д) так, щоб утворилося правильне твердження.
1. Середня лінія трапеції дорівнює
2. Проекція сторони AB на пряму AD дорівнює
3. Висота трапеції дорівнює
А 9 см
Б 12 см
В 15 см
Г 16 см
Д 18 см
Каждый день больной заражает четырех человек, каждый из которых, начиная со следующего дня, каждый день также заражает новых четырех и так далее. Болезнь длится 14 дней. В первый день месяца в город N приехал заболевший гражданин К, и в это же день он заразил четырех человек. В какой день станет 3125 заболевших? (В ответе укажите только число.)
Відповідь: ,.
Марійка зірвала на клумбі 9 нарцисів та 4 тюльпани. Скільки всього існує способів вибору із цих квітів 3 нарцисів та 2 тюльпанів для букета?
Відповідь: ,.
В прямоугольной системе координат в пространстве заданы векторы 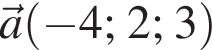 и
и 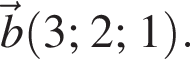 Обчисліть скалярний добуток
Обчисліть скалярний добуток ![]()
Відповідь: ,.
Визначте найменше ціле значення a, за якого один із коренів рівняння
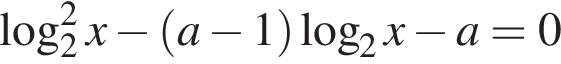
належить проміжку (30; 100).
Відповідь: ,.

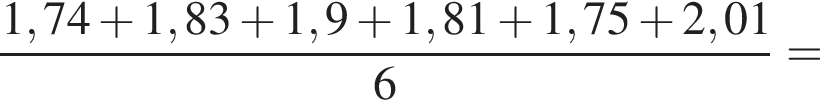
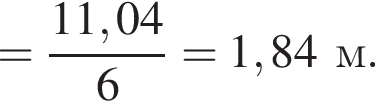
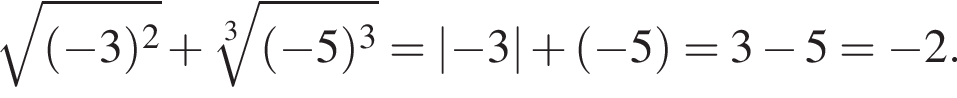
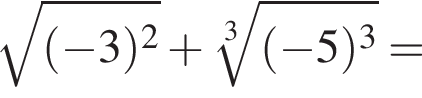
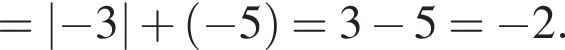
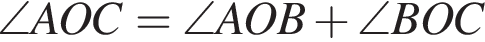 ,
, 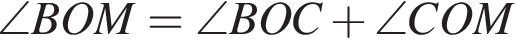 и
и  . Таким образом:
. Таким образом:
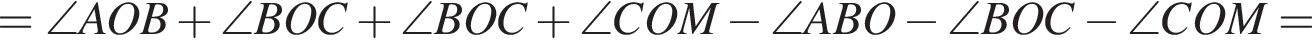
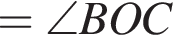
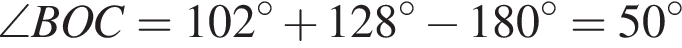 .
.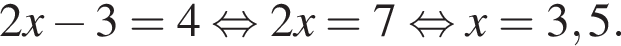
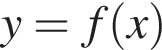 возрастает при
возрастает при 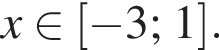
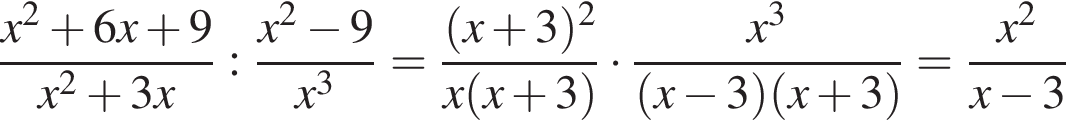
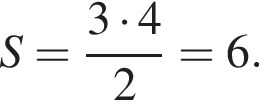
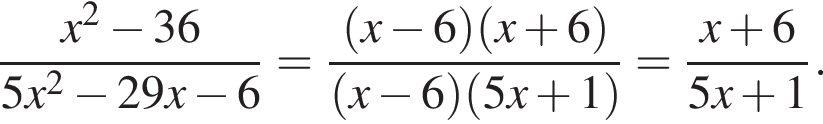
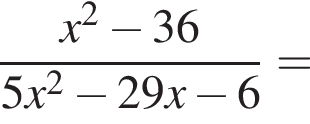
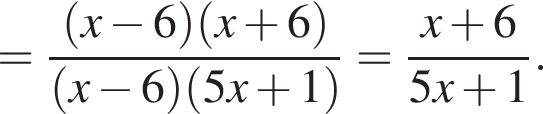
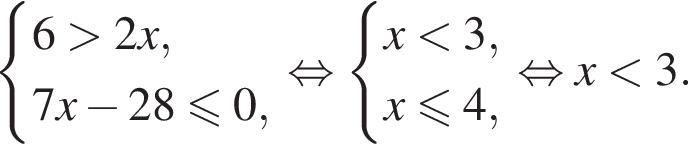
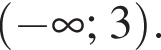
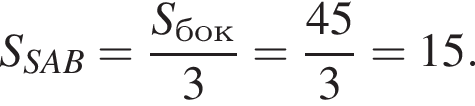
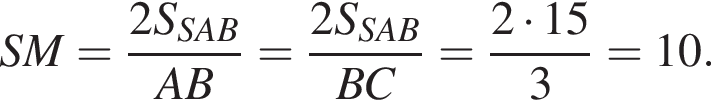
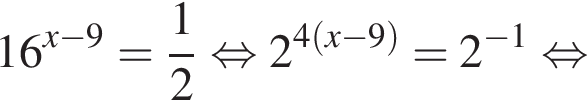
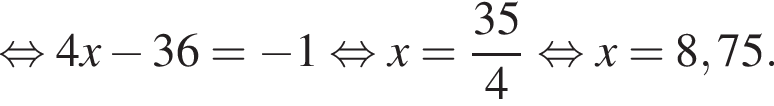
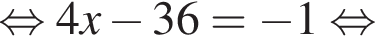

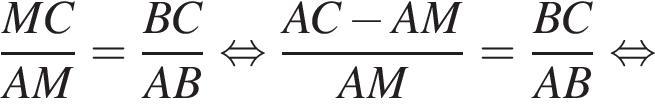
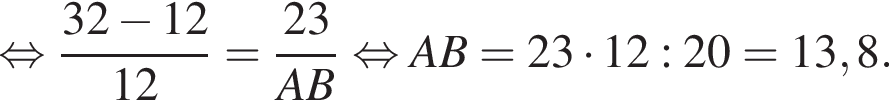
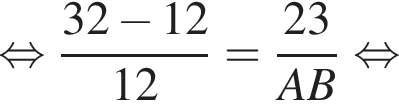
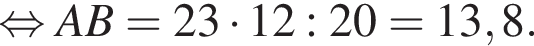
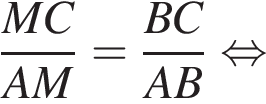
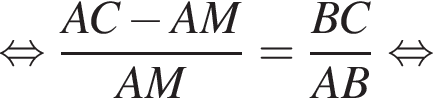
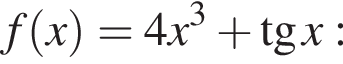
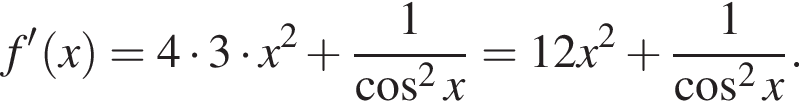
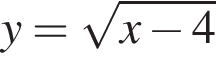 не определена в точке
не определена в точке 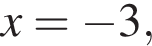 оно равно 1. Таким образом, 2 — Г.
оно равно 1. Таким образом, 2 — Г.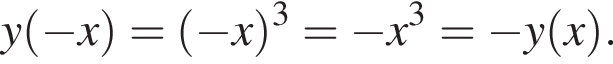 Следовательно, 3 — Д.
Следовательно, 3 — Д.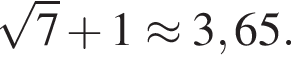 Данное значение соответствует промежутку
Данное значение соответствует промежутку 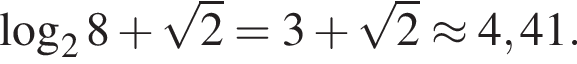 Данное значение соответствует промежутку
Данное значение соответствует промежутку 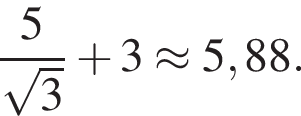 Данное значение соответствует промежутку
Данное значение соответствует промежутку 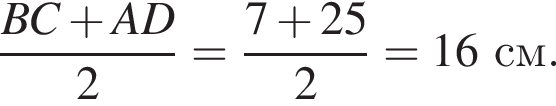
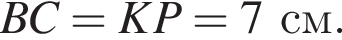 Найдем длину AK:
Найдем длину AK: 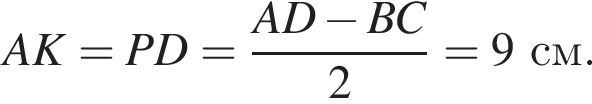
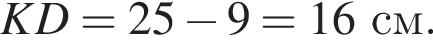

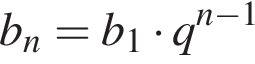 получаем:
получаем: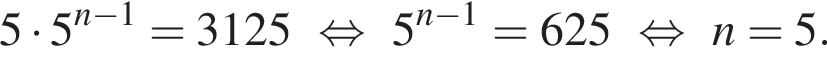
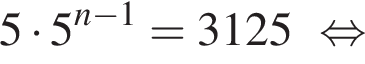
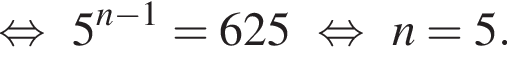
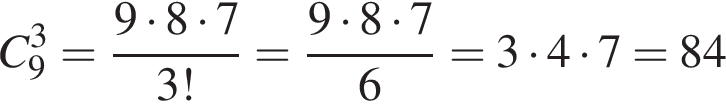
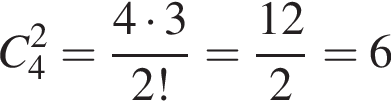 способов выбрать два тюльпана из четырех. Любой из первых способов можно совместить с любым из вторых, поэтому общее число способов равно
способов выбрать два тюльпана из четырех. Любой из первых способов можно совместить с любым из вторых, поэтому общее число способов равно 
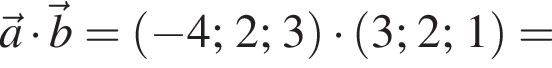
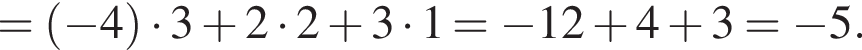
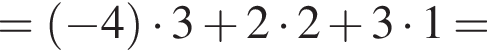
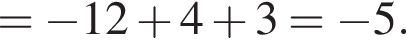
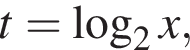 тогда исходное уравнение записывается в виде
тогда исходное уравнение записывается в виде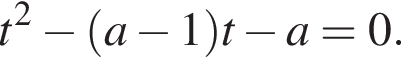
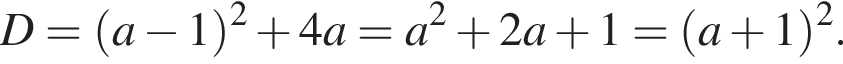
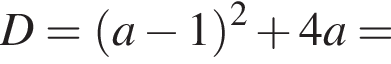
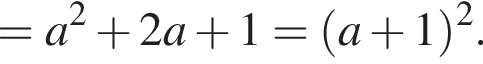
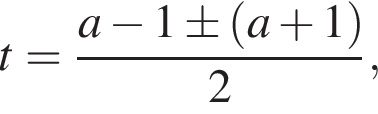 откуда
откуда  или
или 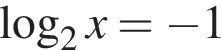 или
или 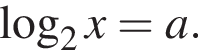 Из первого уравнения
Из первого уравнения 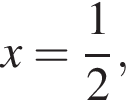 этот корень не лежит в интервале (30; 100). Из второго уравнения
этот корень не лежит в интервале (30; 100). Из второго уравнения 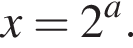 Найдем наименьшее целое значение a, при котором корень этого уравнения принадлежит интервалу (30; 100):
Найдем наименьшее целое значение a, при котором корень этого уравнения принадлежит интервалу (30; 100):