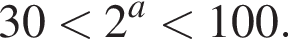На круговій діаграмі показано розподіл посівних площ під зернові культури в агрогосподарстві. Скільки гектарів відведено під гречку, якщо вівсом засіяно на 390 га більше, ніж житом?
Кисть, яка коштувала 240 рублів, продається з 25% знижкою. При покупці двох таких пензлів покупець віддав касиру 500 рублів. Скільки рублів здачі він має отримати?
Через середню лінію основи трикутної призми проведено площину, паралельну бічному ребру. Площа бічної поверхні відсіченої трикутної призми дорівнює 8. Знайдіть площу бічної поверхні вихідної призми.
На малюнку дві прямі перетинаються у точці О. Якщо
 то кут BOC дорівнює:
то кут BOC дорівнює:
Найдите значение выражения 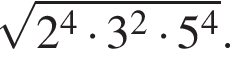
Розв’яжіть рівняння: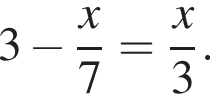
Знайдіть відстань від точки A з координатами (6; 8) до початку координат.
Вкажіть номер малюнка, на якому представлений ескіз графіка функції y = 1 − ( x + 3) 2 .
Які з наведених тверджень є правильними?
I. Діагоналі будь-якого ромба ділять його кути навпіл.
II. Діагоналі будь-якого чотирикутника точкою перетину діляться навпіл.
III. Діагоналі будь-якого квадрата перпендикулярні.
Скоротіть дріб 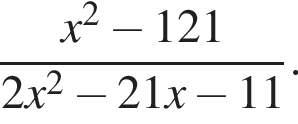
Вкажіть номер малюнка, на якому показано розв’язок системи нерівностей 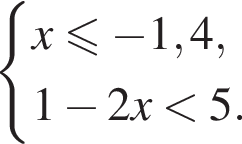
У прямокутнику відстань від точки перетину діагоналей до меншої сторони на 1 більша, ніж відстань від неї до більшої сторони. Периметр прямокутника дорівнює 28. Знайдіть меншу сторону прямокутника.
В арифметичній прогресії (an) 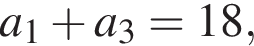 різниця d = −4. Визначте перший член a1 цієї прогресії.
різниця d = −4. Визначте перший член a1 цієї прогресії.
На рисунку зображено фрагмент розгортки правильної чотирикутної призми, утворений з двох її сусідніх граней. Використовуючи зазначені на рисунку розміри, обчисліть площу повної поверхні цієї призми.
Укажіть кількість коренів рівняння 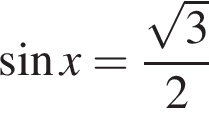 на відрізку [0; 3π].
на відрізку [0; 3π].
Доберіть до функції (1–3) ескіз її графіка (А–Д).
1. 
2. 
3. 
Установіть відповідність між числовим виразом (1−4) та проміжком (А−Д), якому належить його значення.
1. 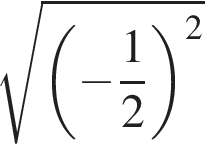
2. ![]()
3. 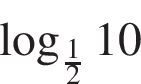
4. 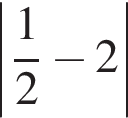
А 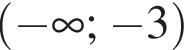
Б [−3; 0)
В [0; 1)
Г [1; 3)
Д 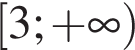
На рисунку зображено відрізок d на координатній площині. Установіть відповідність між відрізком (1–3) та рисунком (А–Д), на якому він зображений.
Відрізок
1. Відрізок, симетричний відрізку d відносно oсі x
2. Відрізок, симетричний відрізку d відносно осі y
3. Відрізок, симетричний відрізку d відносно точки O
Малюнок
Які з наведених тверджень є правильними?
I.Чи вірно, що прямі a і b перетинаються, якщо кожна з цих прямих перетинається з прямою с?
II. Чи вірно, що прямі a та b перетинаються, якщо пряма b перетинається з прямою c, а пряма c перетинається з прямою a?
III. Чи вірно, що прямі a та b перетинаються, якщо пряма a перетинає площину, паралельну до прямої b?
Михайло отримав з математики в першому семестрі такі оцінки: «8», «7», «9», «8». Яку кількість оцінок «10» протягом цього семестру треба отримати Михайлові з математики, щоб середнє арифметичне всіх отриманих у першому семестрі оцінок із цього предмета дорівнювало 9,5? Уважайте, що інших оцінок із математики, окрім «10», Михайло не отримуватиме.
Відповідь: ,.
У прямокутному паралелепіпеді 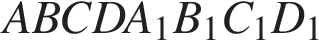 ребро
ребро 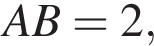 ребро
ребро  ребро
ребро 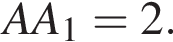 Точка K - середина ребра
Точка K - середина ребра ![]() Знайдіть площу перерізу, що проходить через точки
Знайдіть площу перерізу, що проходить через точки ![]()
![]() і
і ![]()
Визначте найменше ціле значення a, за якого один із коренів рівняння
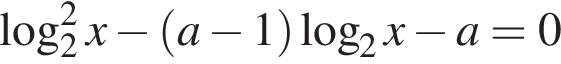
належить проміжку (30; 100).
Відповідь: ,.

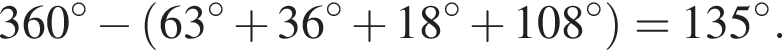 Известно, что длины дуг пропорциональны посевным площадям. Пусть x — площадь, засеянная рожью. Тогда
Известно, что длины дуг пропорциональны посевным площадям. Пусть x — площадь, засеянная рожью. Тогда 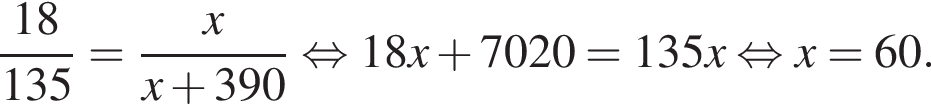
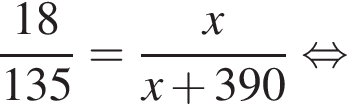
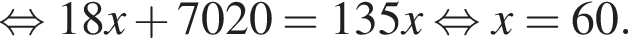


 равна 360°, поэтому
равна 360°, поэтому 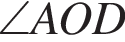 равен 50°. Углы
равен 50°. Углы 
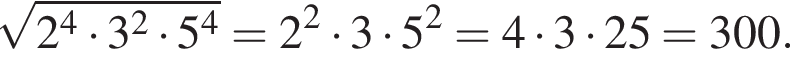
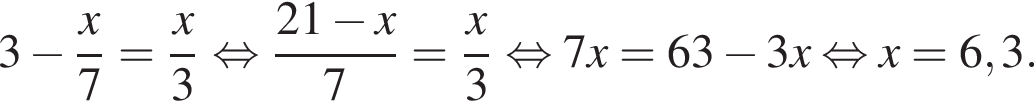
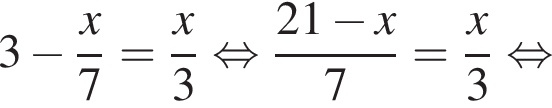
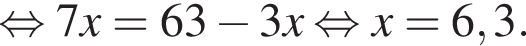
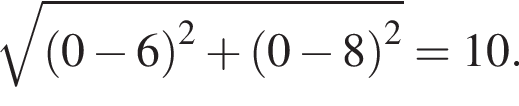
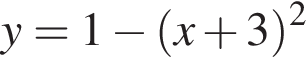 представляет собой параболу, ветви которой направлены вниз, вершина которой сдвинута на 3 единицы влево и на 1 единицу вверх. Таким образом, эскиз графика функции
представляет собой параболу, ветви которой направлены вниз, вершина которой сдвинута на 3 единицы влево и на 1 единицу вверх. Таким образом, эскиз графика функции 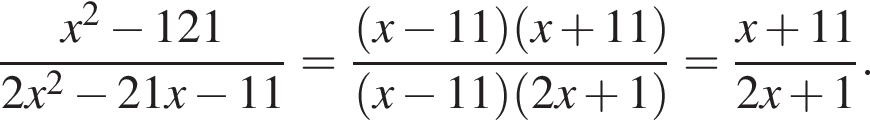
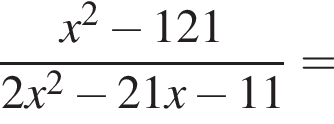
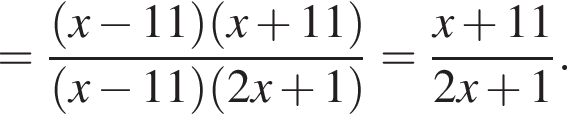
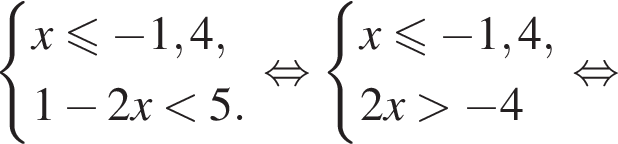
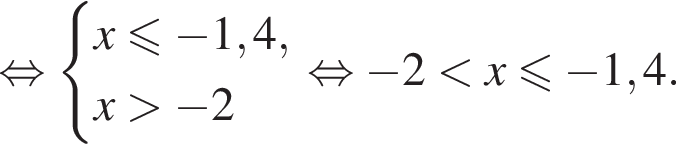
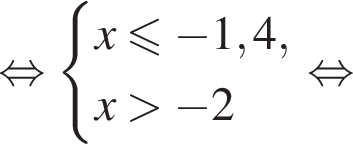
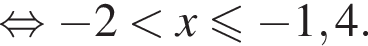
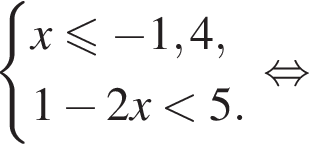
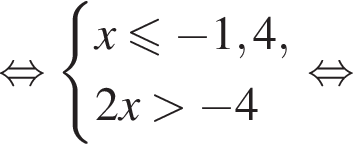
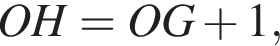 то
то 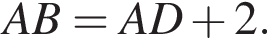 Тогда
Тогда

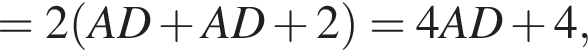
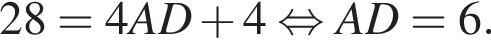
 и
и 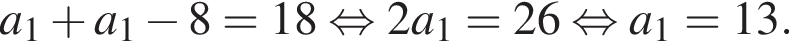
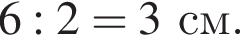 Тогда площадь полной поверхности равна
Тогда площадь полной поверхности равна 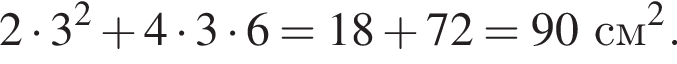
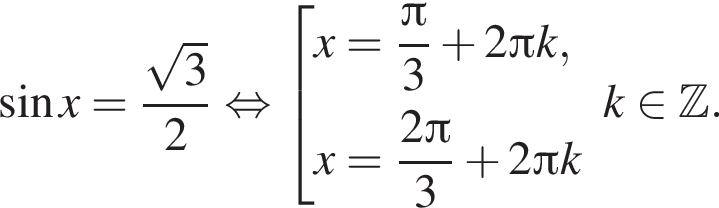
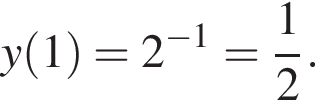 График, содержащий точку
График, содержащий точку 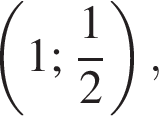 очевидно, может быть только график Б.
очевидно, может быть только график Б.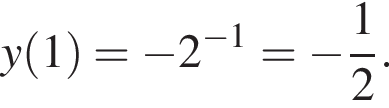 График, содержащий точку
График, содержащий точку 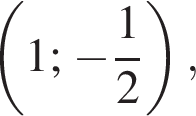 очевидно, может быть только график Д.
очевидно, может быть только график Д.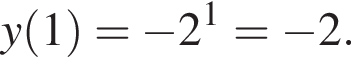 График, содержащий точку
График, содержащий точку 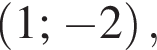 очевидно, может быть только график А.
очевидно, может быть только график А.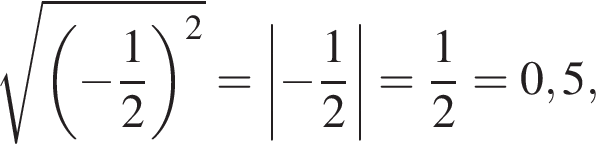
 Получаем, что 1 — B.
Получаем, что 1 — B.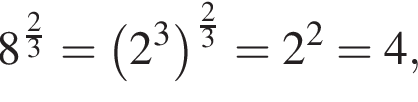 где
где 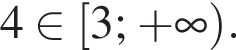 Итак, 2 — Д.
Итак, 2 — Д. 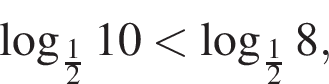 где
где 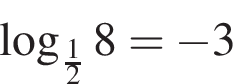 и
и 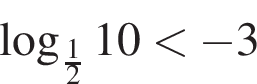 при
при 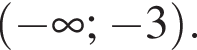 Следовательно, 3 — A.
Следовательно, 3 — A.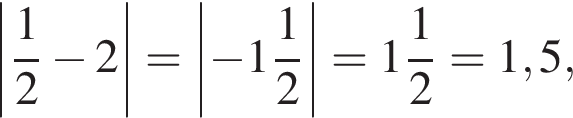
 Следовательно, 4 — Г.
Следовательно, 4 — Г.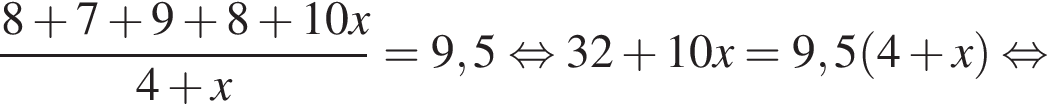
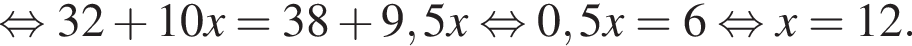
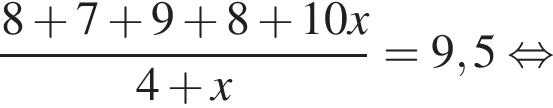

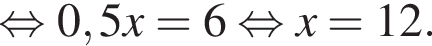

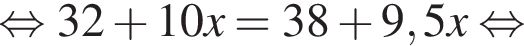
 — параллелограмм. Кроме того, ребро
— параллелограмм. Кроме того, ребро 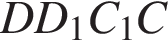 и
и 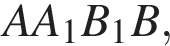 поэтому углы
поэтому углы 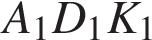 и
и 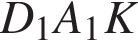 — прямые. Следовательно, сечение
— прямые. Следовательно, сечение 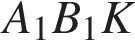 по теореме Пифагора найдем
по теореме Пифагора найдем 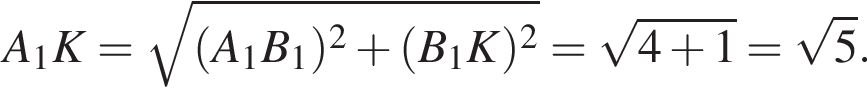
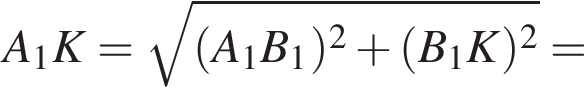
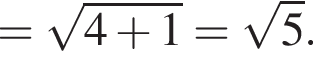

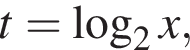 тогда исходное уравнение записывается в виде
тогда исходное уравнение записывается в виде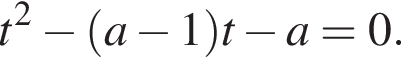
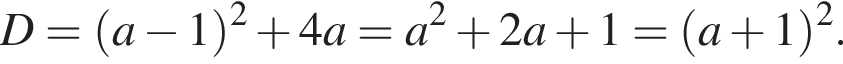
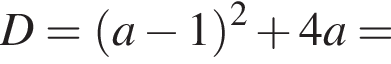
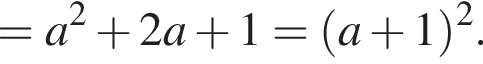
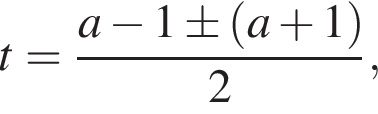 откуда
откуда  или
или 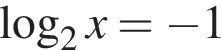 или
или 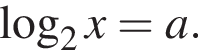 Из первого уравнения
Из первого уравнения 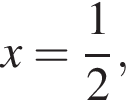 этот корень не лежит в интервале (30; 100). Из второго уравнения
этот корень не лежит в интервале (30; 100). Из второго уравнения 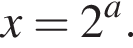 Найдем наименьшее целое значение a, при котором корень этого уравнения принадлежит интервалу (30; 100):
Найдем наименьшее целое значение a, при котором корень этого уравнения принадлежит интервалу (30; 100):